Polar to Cartesian Conversions
· Zynh LudwigThe Problem
Often times when working in a 2D display framework you want to display things in a circular pattern. However you find yourself unable to because you don’t know what magical combination of x and y will find you along the circles edge, curses to the cartesian lords.
A Solution
Hail be the wonderful forces of pre-calculus teachers the world over. Polar coordinates are what we want! They allow us to define an angle and a radius to identify a point in 2D space, rather than x and y.
But how do we use this wonderful coordinate system on a webpage?\ Wellllll, that’s the catch. You can’t directly. However all of the tools necessary to convert from Polar coordinates to cartesian coordinates are available in native javascript.
The only tools needed for the conversion are Math.cos(), Math.sin() and a circle constant, which is a whole discussion I’d be willing to have, but we don’t have Math.TAU yet, so at the top of our file we will use Math.TAU = 2*Math.PI as it makes our equations cleaner. Tau manifesto
For any polar coordinate where r = radius and theta = angle then we can convert to cartesian as simply as;
let x = r * Math.cos(theta);
let y = r * Math.sin(theta);Example
Lets say we want to get the center positions of 20 circles arranged in a circle about 0, 0. As seen in the p5 sketch seen below. Link to sketches code
All we need to do is divide the number of radians in a circle by 20, to get the angle at each increment evenly spaced apart. Then loop through those increments and draw circles.
Math.TAU = 2 * Math.PI; // Math.TAU makes our code a hair cleaner,
// and I am astonished its not a language feature yet
let n = 20; // Number of circles
let r = 100; // 100px radius
for (let i = 0; i < n; i++) {
let theta = (Math.TAU / n) * i;
let x = r * Math.cos(theta);
let y = r * Math.sin(theta);
drawCircle(x, y); // Assuming this is your method
// for drawing a circle at position x, y
}Conclusion
Polar coordinates are a powerful tool for converting from Polar coordinates radius and angle to cartesian coordinates x and y
Not a perfect visualization, but the angle of the black line in radians is Θ and the radius is 1
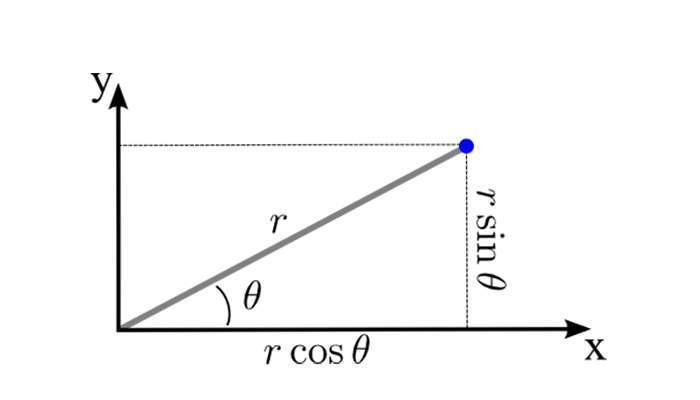
Image shamelessly ripped from
Linear motion tips